|
|
|
| 12/5(木) 13:25-15:00 |
| コーディネータ:諏訪正樹(オムロン)
|
|
|
IS1-E1
|
三次元物体の位置・姿勢推定のための螺旋状特徴の提案
|
| |
○吉村裕一郎,青木公也(中京大)
|
概要:本研究では,乱雑な三次元シーンへの適用を想定した物体の位置・姿勢推定のためのアルゴリズムを提案する.エリア深度センサから得られたPoint Cloudデータを基に,物体表面の形状データを求める.物体表面上の任意点を中心に近傍領域のデータを螺旋状に取得することで,局所特徴が周期的に表れる波形として表現した,螺旋状特徴量(SSF)を提案する.SSFは,注目点を基点とした方向と距離の情報を統合した軸に対応した表面特徴(今回は点の方向)の分布を表す.したがって,予め登録してある1点の対応が分かれば物体の位置・姿勢を6自由度で算出することが可能であり,オクルージョンへの対応が期待される.
<キーワード>Point Cloudデータ, 位置・姿勢推定, 螺旋状特徴
|
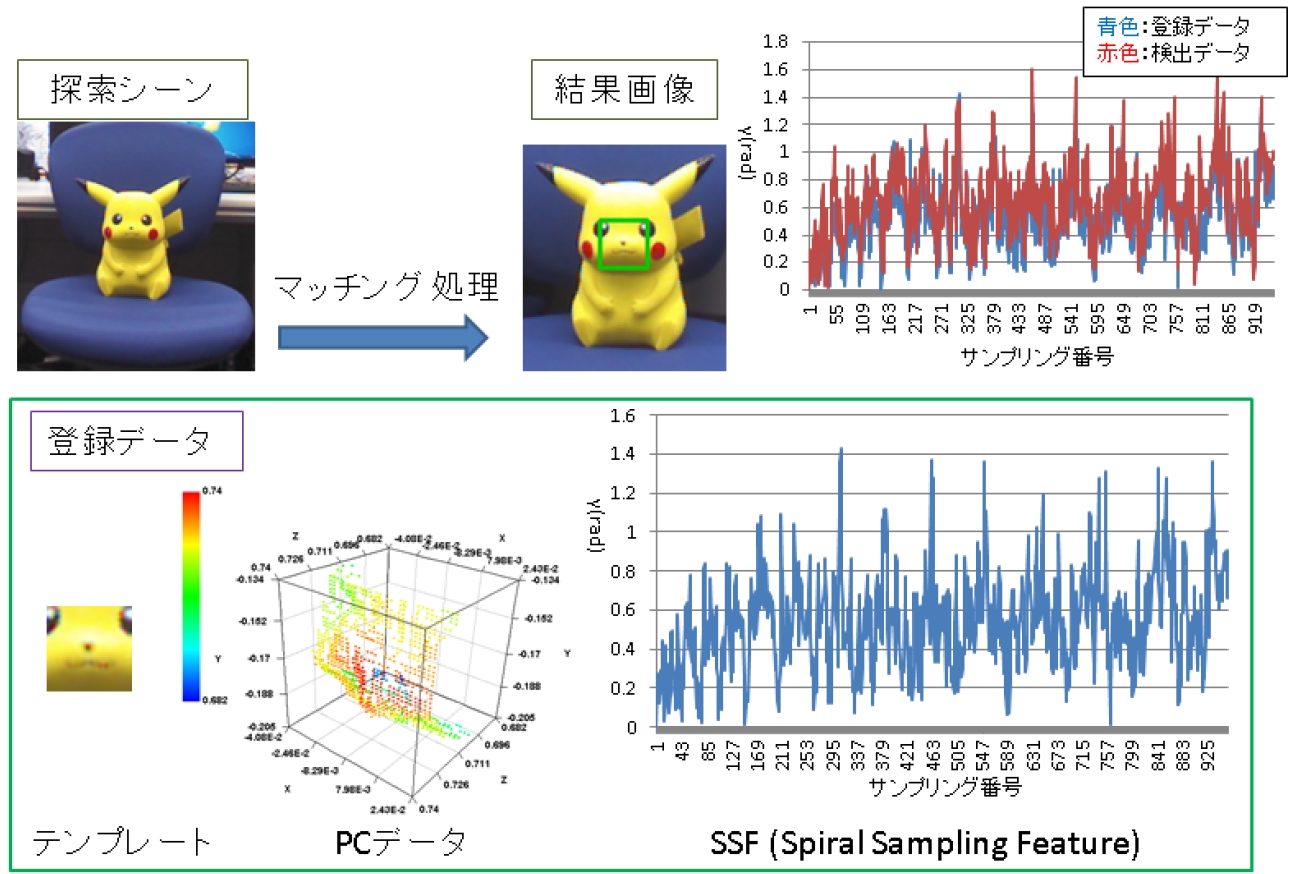
SSFの検出
|
|
IS1-E2
|
外観・形状マッチングによる位置・姿勢推定手法の検討
|
| |
○野口遼,山崎太郎,中村明生(東京電機大)
|
概要:物体の外観と形状に基づいて位置・姿勢を推定する手法を提案する.形状とテクスチャ情報を持った3次元モデルから多視点のモデル画像とモデル点群を生成する.それらをノードとする探索木を探索し,SIFT特徴を用いて環境画像とモデル画像の外観マッチング,FPFH特徴を用いて環境点群とモデル点群の形状マッチングを行う.マッチングの誤対応をRANSACで排除し,外観と形状2通りのマッチングで得られた対応点を統合して用いることで位置・姿勢推定を行う.検証実験により,平均回転誤差5[deg],平均並進誤差4[mm]で位置・姿勢推定が行えることを確認した.
<キーワード>3次元物体認識,位置・姿勢推定,ボクセルマッチング
|

位置・姿勢推定結果
|
|
IS1-E3
|
Kinectによるラジオ体操評価システムの設計
|
| |
○野々口誠人,藤原竜也,田中雅博(甲南大)
|
概要:ラジオ体操はどこでもできる運動として広く行われているが,きちんと体操がで
きているかどうかの判定は困難である.本研究では,RGB-D センサであるKinect
SDK for Windows の関節検出機能を用いて,動作の評価システムの設計を行い,
SDKで得られた3次元位置により,各関節間の3次元角度から運動動作を評価する.
今回は,チャプター1の部分について,評価実験を行った.
<キーワード>ラジオ体操,Kinect,運動動作評価システム
|

|
|
IS1-E4
|
デプスセンサによる路面と壁面の検知方法
|
| |
○田中雅博(甲南大)
|
概要:筆者は,姿勢が安定しないデプスセンサで安定的に路面を検出する手法を既に提案している.本稿では,それに加えて,壁面を検出する方法を提案する.これにより,近くにある障害物が壁なのかどうか,壁であれば,面の向きといった,詳細を知ることができる.実験により,壁面の検出結果を示す.このシステムは,歩行や自動運転の助けになるほか,3次元SLAMへの応用も可能である.
<キーワード>デプスセンサ,路面と壁面検知,拡張カルマンフィルタ
|

|
|
IS1-E5
|
仮想視点画像を用いた良視点位置からの運動物体追跡と物体認識
|
| |
○根来秀多,望月優介,青木公也(中京大)
|
画像処理において対象物体を撮像する視点位置は重要である.本研究では,運動物体追跡,
物体認識に対する良視点の位置・方向について考察した.運動物体追跡では,対象物体が静止
して見える視点,物体認識では,テンプレートと見え方が等しい視点が良視点であると考えられる.
これに対して,Point Cloud データを使用して仮想的に複数の視点を生成し,良視点の選択と汎
用画像処理を組み合わせる手法を提案する.図より,提案手法では対象物体(クマ)が高速移動し
た場合も見失うこと無く追跡できている.
<キーワード>仮想視点,Point Cloud データ,物体追跡,テンプレートマッチング
|

追跡結果
|
|
IS1-E6
|
Growing Neural Gasに基づく3次元点群処理
|
| |
○戸田雄一郎,久保田直行(首都大)
|
概要:近年,Virtual Reality 技術やAugmented Reality 技術の発展とともに,3 次元画像処理への期
待が高まってきている.特に,Microsoft から,カメラ画像と3次元距離データが同時取得可能なKinect
が発売されて以来,様々な3 次元点群処理技術が提案・提供されている.これらの3 次元点群処理技
術において,重要な技術の中に (i)ダウンサンプリング,(ii)法線ベクトルの算出,(iii)オブジェクトのクラ
スタリングが存在する.本稿では,教師なし学習の1 つであるGrowing Neural Gas (GNG)を色情報を持
った3 次元点群データに適用することにより, 3 次元点群処理を行う手法の提案をする.
<キーワード>3次元点群処理,計算知能,自己組織化
|

本手法の結果
|
|
IS1-E7
|
位相シフト法におけるパターン輝度補正手法の評価
|
| |
○加藤嗣,田口亮(名工大),保黒政大(中部大),
梅崎太造(名工大)
|
概要:我々は高精度な三次元形状計測システムを,市販のプロジェクタとカメラおよび計算機を用
いることで安価に構築することを目指している.その際に課題となるのは,市販プロジェクタの明る
さの再現性の問題により,意図しない照度で計測対象が照らされ,計測精度が低下することであり,
その対策として汎用的な補正手法を提案した.また,提案手法の汎化性を確認するため,複数の
プロジェクタで効果を確認した.使用プロジェクタの光源の明るさが小さい場合,有効であり最大
47[%]の精度向上が確認されたが,大きい場合は精度低下が確認され,周期性のあるノイズが発
生した.時間変動による光源ノイズによる影響が考えられ,今後の課題である.
<キーワード>位相シフト法,プロジェクタ,三次元形状計測,パターン補正
|
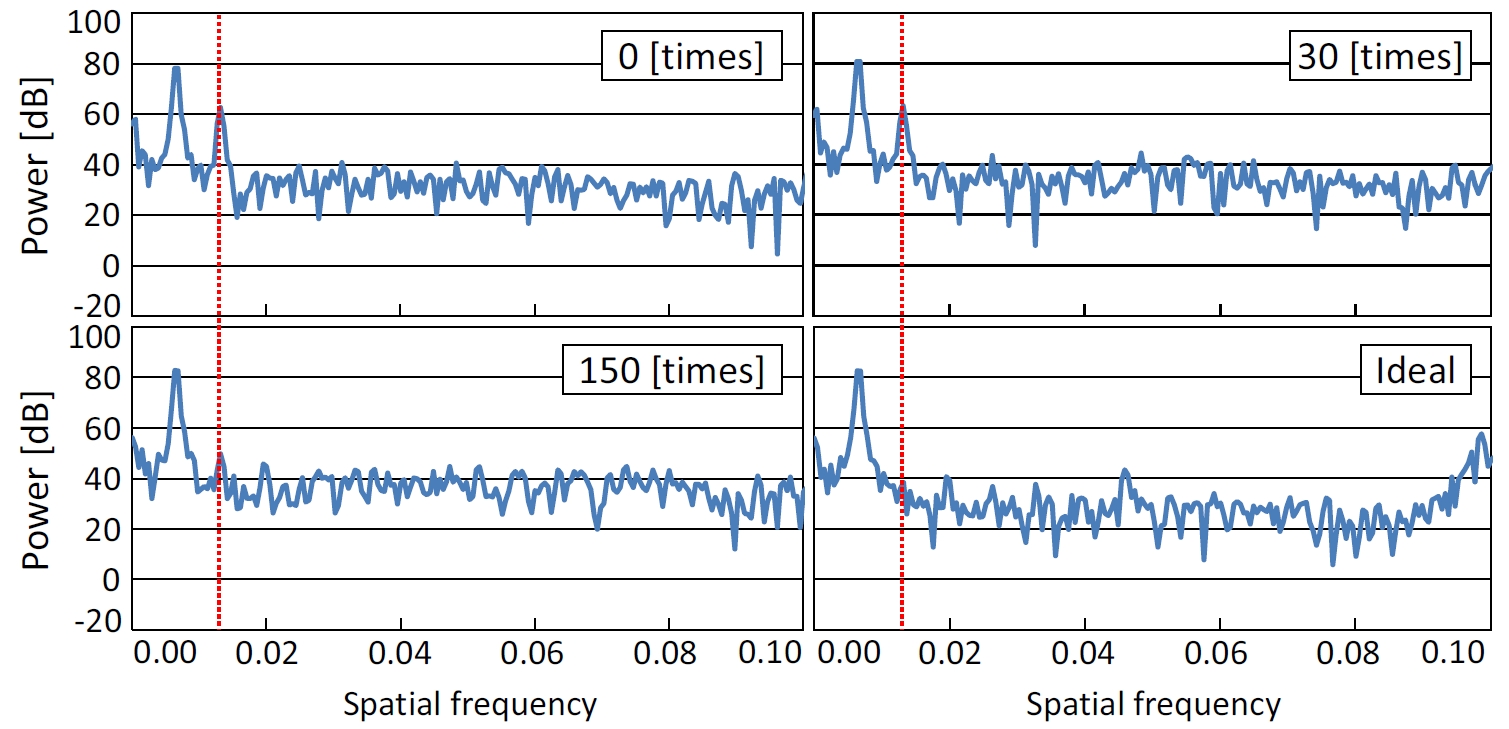
補正後正弦波の周波数解析結果
|
|
IS1-E8
|
位相シフト法を用いた航空機主翼ファスナ計測
|
| |
○鈴木貴大,加藤嗣,田口亮(名工大),保黒政大(中部大),
梅崎太造(名工大)
|
概要:航空機主翼のファスナ装着状態は,機体の安全性に大きく関わる.そのため,装着状態の検査が必要となる.現在は,検査員がファスナ装着状態を手作業で確認しているため,非効率的である.そこで,自動非接触検査による検査効率の向上を目的とし,カメラとプロジェクタを用いた三次元計測による自動検査手法の提案をする.計測手法の有用性を検討するとともにファスナ計測精度向上を目的とした手法を考案する.本手法を用いてファスナを計測した精度は傾きが最大誤差0.27[deg],深さが最大誤差0.07[mm]である.
<キーワード>三次元計測,位相シフト法,航空機用ファスナ,外観検査
|

ファスナサンプル,計測環境
|
|
IS1-E9
|
複数のレーザスポットを用いた非点収差による三次元計測
|
| |
○尾崎裕章,ウキエツ,加藤嗣,田口亮(名工大),保黒政大(中部大),
堀米秀嘉(ホーリーマイン),梅崎太造(名工大)
|
概要:工業製品の精密不良検査などの増加に伴い,高精度な三次元計測器に対する需要が増加している.しかし既存の三次元計測器は時間を要するため対象の位置ずれにより計測誤差が大きくなる問題がある.本研究では高速かつ高精度な三次元計測を実現するためにマルチスポットレーザおよび非点収差に用いる屈折の異なる2種類のレンズにより光学システムを構成して計測手法の検証を行う.平面の繰り返し計測結果より0.054 [mm]の誤差で計測可能であることを確認した.
<キーワード>光学システム,非点収差,三次元計測
|

実験装置外観
|
|
IS1-E10
|
全空間テーブル化手法を用いた形状計測における縮小投影と位相平滑化の精度評価
|
| |
○柾谷明大,森本吉春,高木哲史(4Dセンサー)
|
概要:Whole-space tabulation method is a technique to relate phase of projected grating with coordinates of the corresponded point pixel by pixel. The relation data are stored in a table. Thereby, high speed and accurate shape measurement is realized. In this paper, a reduced size projector and phase difference smoothing method is developed. An experiment to evaluate this equipment is performed. The shape measurement accuracy using the new equipment is better.
<キーワード>全空間テーブル化手法,縮小投影,位相平滑化
|
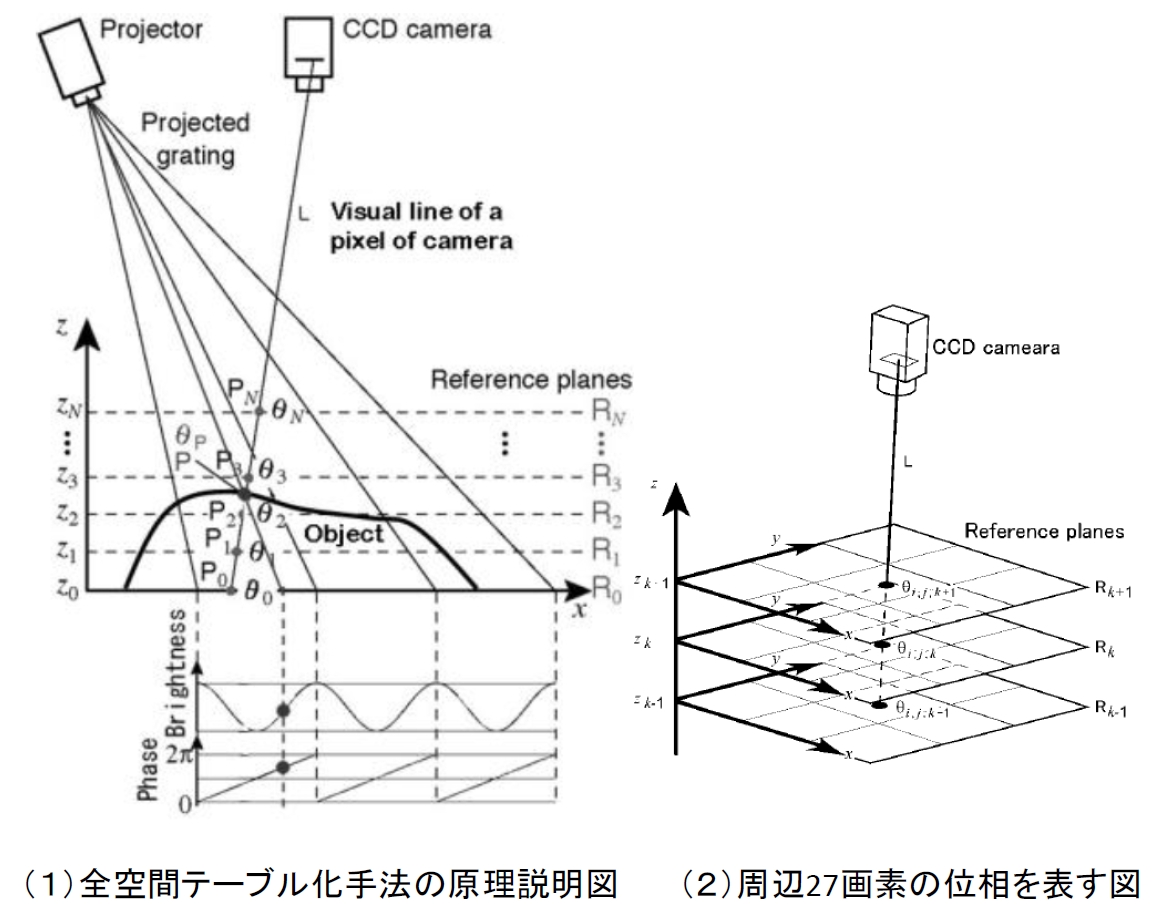
全空間テーブル化手法の原理説明図
|











